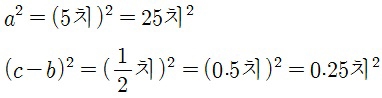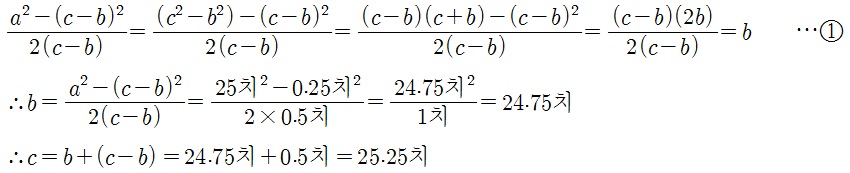| 조선시대의 수학 문제와 풀이법(4) |
|
| |||
| |||
|
|
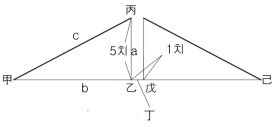 위 예제를 그림으로 나타내면 왼쪽과 같다. 甲己가 문지방, 甲丙이 문 한짝의 너비이다. 따라서 甲己의 절반인 甲丁이 甲丙과 같다. 乙丙은 문지방부터 열린 문 끝까지의 거리이고, 乙戊는 양쪽 문이 벌어진 거리이다.
이 예제는 결국 직각삼각형 甲乙丙의 높이(乙丙, a)와 ‘빗변-밑변(甲丙-甲乙, c-b)’를 알 때 빗변(甲丙, c)을 구하는 기하학 문제이다. 이는 『구장산술(九章算術)』 「구고장(句股章)」 열째 문제를 계승한 것으로, 『구일집』과 『구장산술』의 풀이를 현대 수식 기호를 사용해 정리하면 다음과 같다.
주어진 a와 (c-b)의 길이로부터, 위 예제를 그림으로 나타내면 왼쪽과 같다. 甲己가 문지방, 甲丙이 문 한짝의 너비이다. 따라서 甲己의 절반인 甲丁이 甲丙과 같다. 乙丙은 문지방부터 열린 문 끝까지의 거리이고, 乙戊는 양쪽 문이 벌어진 거리이다.
이 예제는 결국 직각삼각형 甲乙丙의 높이(乙丙, a)와 ‘빗변-밑변(甲丙-甲乙, c-b)’를 알 때 빗변(甲丙, c)을 구하는 기하학 문제이다. 이는 『구장산술(九章算術)』 「구고장(句股章)」 열째 문제를 계승한 것으로, 『구일집』과 『구장산술』의 풀이를 현대 수식 기호를 사용해 정리하면 다음과 같다.
주어진 a와 (c-b)의 길이로부터,
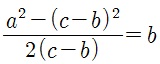 의 유도 과정 ①은 전통 산학서에는 본디 감추어진 것을 독해의 편의를 위해 필자가 잠깐 보충한 것이다.)
구고정리는 직각삼각형의 세 변 사이에 ‘c2=a2+b2 ’의 관계가 성립한다는 기하학의 기본 명제로, 흔히 피타고라스정리로 불리는 것이다. 이 정리에 대한 초보적인 지식은 B.C.2000년경 고대 이집트인들에게 이미 알려져 있었다. B.C.1700년경 바빌로니아인들은 (119, 120, 169), (3367, 3456, 4825), (4601, 4800, 6649) 등 이 관계를 만족하는 자연수 쌍을 경험적으로 찾아나갔고, 중국에서도 B.C.1000년경까지 거슬러 올라가는 『주비산경(周髀算經)』의 내용에 이미 언급되었다. 그런데도 이 정리가 피타고라스(Pythagoras, B.C.580년경~B.C.490년경)의 이름으로 불리는 것은 그가 각별히 중시하고 부각했기 때문이다. 피타고라스가 이 정리를 중시한 것은 실은 우주 자연의 조화를 모두 자연수의 비(比)로 설명하려 한 그의 수 신비주의(數神秘主義) 입장과 맥을 같이 하는 것이었다.
기록으로 확인되는 이 정리의 완전한 증명이 서양에서는 그리스 유클리드(Euclid, B.C.330~B.C.275)의 『기하학원론Elements』에서, 동양에서는 삼국시대 위(魏)나라 유휘(劉徽)의 『구장산술주(九章算術注)』에서 처음 보인다. 유클리드는 ‘밑변과 평행한 선분 위에 꼭지점을 둔 삼각형은 모두 면적이 같다.’라는 기하학 지식을 바탕으로 면적을 비교하여 증명하였다. 자세한 사항은 웹 검색을 통해 어렵지 않게 찾아볼 수 있다.
유휘는 그림과 설명을 함께 사용하여 증명했으나 지금은 다음과 같은 설명만 남아 있다.
“구(句)의 제곱은 붉은색 정사각형 면적이 되고, 고(股)의 제곱은 푸른색 정사각형 면적이 된다. 같은 모양의 면적끼리 내보내고 들여놓아 서로 벌충하고, 그 나머지는 이동하지 않는다. 이렇게 하면 두 정사각형 면적의 합이 현(弦)을 한 변으로 하는 정사각형의 면적이 된다.[句自乘 爲朱方 股自乘 爲青方 令出入相補 各從其類 因就其餘 不移動也 合成弦方之幂]” 의 유도 과정 ①은 전통 산학서에는 본디 감추어진 것을 독해의 편의를 위해 필자가 잠깐 보충한 것이다.)
구고정리는 직각삼각형의 세 변 사이에 ‘c2=a2+b2 ’의 관계가 성립한다는 기하학의 기본 명제로, 흔히 피타고라스정리로 불리는 것이다. 이 정리에 대한 초보적인 지식은 B.C.2000년경 고대 이집트인들에게 이미 알려져 있었다. B.C.1700년경 바빌로니아인들은 (119, 120, 169), (3367, 3456, 4825), (4601, 4800, 6649) 등 이 관계를 만족하는 자연수 쌍을 경험적으로 찾아나갔고, 중국에서도 B.C.1000년경까지 거슬러 올라가는 『주비산경(周髀算經)』의 내용에 이미 언급되었다. 그런데도 이 정리가 피타고라스(Pythagoras, B.C.580년경~B.C.490년경)의 이름으로 불리는 것은 그가 각별히 중시하고 부각했기 때문이다. 피타고라스가 이 정리를 중시한 것은 실은 우주 자연의 조화를 모두 자연수의 비(比)로 설명하려 한 그의 수 신비주의(數神秘主義) 입장과 맥을 같이 하는 것이었다.
기록으로 확인되는 이 정리의 완전한 증명이 서양에서는 그리스 유클리드(Euclid, B.C.330~B.C.275)의 『기하학원론Elements』에서, 동양에서는 삼국시대 위(魏)나라 유휘(劉徽)의 『구장산술주(九章算術注)』에서 처음 보인다. 유클리드는 ‘밑변과 평행한 선분 위에 꼭지점을 둔 삼각형은 모두 면적이 같다.’라는 기하학 지식을 바탕으로 면적을 비교하여 증명하였다. 자세한 사항은 웹 검색을 통해 어렵지 않게 찾아볼 수 있다.
유휘는 그림과 설명을 함께 사용하여 증명했으나 지금은 다음과 같은 설명만 남아 있다.
“구(句)의 제곱은 붉은색 정사각형 면적이 되고, 고(股)의 제곱은 푸른색 정사각형 면적이 된다. 같은 모양의 면적끼리 내보내고 들여놓아 서로 벌충하고, 그 나머지는 이동하지 않는다. 이렇게 하면 두 정사각형 면적의 합이 현(弦)을 한 변으로 하는 정사각형의 면적이 된다.[句自乘 爲朱方 股自乘 爲青方 令出入相補 各從其類 因就其餘 不移動也 合成弦方之幂]” 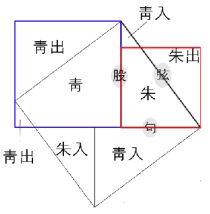 유휘의 이 증명은 ‘같은 면적끼리 내보내고 들여놓아 서로 벌충하는[出入相補]’ 원리가 핵심인데, 이를 이용한 증명 방법으로 30여 가지가 알려져 있다. 지금까지는 청나라 이황(李潢)이 『구장산술세초도설(九章算術細草圖說)』에서 제시한 오른쪽 그림이 유휘가 사용한 그림에 가장 가깝다고 평가되고 있다. 그림을 설명하면 다음과 같다.
句2 =‘붉은 정사각형[朱方]’=주(朱)+주출(朱出)
유휘의 이 증명은 ‘같은 면적끼리 내보내고 들여놓아 서로 벌충하는[出入相補]’ 원리가 핵심인데, 이를 이용한 증명 방법으로 30여 가지가 알려져 있다. 지금까지는 청나라 이황(李潢)이 『구장산술세초도설(九章算術細草圖說)』에서 제시한 오른쪽 그림이 유휘가 사용한 그림에 가장 가깝다고 평가되고 있다. 그림을 설명하면 다음과 같다.
句2 =‘붉은 정사각형[朱方]’=주(朱)+주출(朱出)股2 =‘푸른 정사각형[靑方]’=청(靑)+‘큰 청출(靑出)’+‘작은 청출(靑出)’ 弦2 =‘弦을 한변으로 한 정사각형[弦方]’ =청(靑)+주(朱)+‘작은 청입(靑入)’+주입(朱入)+‘큰 청입(靑入)’ 그런데 다음과 같은 합동 관계가 있으므로, 큰 청출(靑出)=큰 청입(靑入) 작은 청출(靑出)=작은 청입(靑入) 주출(朱出)=주입(朱入) ∴ ‘붉은 정사각형[朱方]’+‘푸른 정사각형[靑方]’=‘弦을 한변으로 한 정사각형[弦方]’ ∴ 구2+고2=현2 구고정리를 증명하는 방법은 닮은 삼각형 또는 면적을 비교하는 기하학적 방법, 대수적 방법, 둘 이상을 겸한 방법 등 여러 가지가 있는데, 유휘의 이 방법은 오로지 면적 비교만을 이용하였다. 그림의 청(靑), 주(朱), 작은 청입(靑入), 큰 청입(靑入), 주입(朱入) 등 5조각을 만들어 칠교놀이를 하듯이 작은 청입(靑入), 큰 청입(靑入), 주입(朱入)의 배치를 달리하는 것만으로 증명이 완성된다. 이와 유사한 조각맞추기 방법은 1837년 영국의 헨리 페리갈도 사용한 바 있다. 피타고라스정리에 대한 증명은 근현대에도 계속 고안되어 300개 이상의 증명법이 존재하며, 이 증명법들을 유형별로 분류하여 수록한 책이 간간이 출간될 만큼 지속적인 관심을 받고 있다. 2300년 전에 이미 명쾌하게 증명된 상황을 생각하면 이 같은 현상은 ‘쓸모’와는 상관없는 ‘유희’로서 기하학을 즐기는 것으로 볼 수 있다. 유휘의 증명에 사용되었던 그림은 과연 이황(李潢)이 추정한 위 그림과 정말로 일치할까? 유휘의 설명에 더 잘 부합하는 그림은 없을까? 유휘와 세월이 공모한 듯 던져놓은 수수께끼에 나만의 해답을 찾아보는 것은 어떨까? |
|
'고전포럼 > 고전명구.산문' 카테고리의 다른 글
| [고전산문] 세상에서 가장 좋은 복 (0) | 2016.11.07 |
|---|---|
| [고전명구] 익숙해질 때까지 (0) | 2016.11.07 |
| [고전산문] 조선의 주축활자 갑인자 (0) | 2016.11.07 |
| [고전명구] 칭찬도 과유불급 (0) | 2016.11.07 |
| [고전산문] 실사구시 (0) | 2016.11.07 |